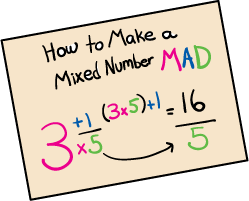I will not be posting this week. I will be at the TCEA Conference in Austin all week.
About Me

- Tina Dittrich
- Welcome to my math blog! The purpose of this blog is to help you stay informed about our learning and experiences that have taken place during our math class. I have also included links your child (and you) may want to use in order to supplement math learning in 5th grade.
Saturday, January 31, 2015
Friday, January 30, 2015
We have made it to the 100th day of school!
We began our day by seeing aged photos of ourselves! We made these using the Aging Booth app. The classes will be using these throughout the day, but I think they enjoyed just seeing each other "old"! Here is my age progression:
In math we had a little fun with the 100 days of school. I found a 100th Day of School Math Goofy Glyph on Teachers Pay Teachers.
My students had a great time answering the 10 math questions and adding the appropriate item to their person cutout! Once the "person" is complete, we will be showcasing them on our lockers.
Thursday, January 29, 2015
Adding and Subtracting Mixed Numbers (continued)
Today we just continued adding and subtracting mixed numbers. After completing the assignment, I asked students to work on Think Through Math.
Don't forget our rewards:
Don't forget our rewards:
- As a 5th grade, we have a goal of Think30. Every student who reaches this goal by April 20, will go to Chuck E. Cheese and a movie with me in May.
- Every time a student passes 5 lessons, their name is added to our chart and they earn a bead for their Outdoor School necklace AND $10 PRIDE bucks to use in the AWEsome store.
- Students have been donating points to earn a class reward from TTM. Two of the classes have opted to earn a pizza party, while the third class has opted to donate $50 to Make A Wish.
- Don't forget night and weekend rewards also! All of the rewards above are earned over nights and weekends, but we also earn $20 PRIDE bucks for every 45 minutes spent working on passing a lesson on TTM, as well as extra credit in the gradebook!
Wednesday, January 28, 2015
Adding and Subtracting Mixed Numbers
We put all of our fraction knowledge to work today. In order to add and subtract mixed numbers, we had to do all of the following:
- First, we had to convert our mixed numbers into improper fractions (p. 26 of our journal)
- Once we had our improper fractions, we needed to determine a common denominator (p. 25 of our journal). This includes:
- making factor trees for our two denominators
- creating a venn diagram to place our prime factors into
- determine our common denominator by multiplying all of the numbers on the venn
- Now that we have a common denominator, we have to make equivalent fractions with our improper fractions.
- Next, we add or subtract.
- Now take the answer, which is still an improper fraction, and turn it back into a mixed number (p. 26 our our journal)
- Now, we need to determine if it can be simplified (p. 25 of our journal). This includes:
- First, seeing if either the numerator or denominator is prime (p. 24 our our journal).
- If it is prime, then see if the other number is a multiple and divide by it.
- If it isn't prime then we need to find our greatest common factor.
- To find our greatest common factor:
- make factor trees for our numerator and denominator
- create a venn diagram to place our prime factors into
- any numbers in the center section of the venn need to be multiplied together, this is the GCF
- Once we have the GCF, the numerator AND denominator need to be divided by that number
We followed this procedure on our assignment, "A Magical Getaway." I found this worksheet in The Mailbox Magazine, Dec/Jan, 2011 issue, p. 12. To view the first four problems being solved, please watch: Adding and Subtracting Mixed Numbers.
Tuesday, January 27, 2015
Monday, January 26, 2015
Mixed Numbers and Improper Fractions
We worked with Mixed Numbers and Improper Fractions today. We began by taking notes and making a foldable for our math journals.
First, we focused on Mixed Numbers to Improper Fractions. To see our notes, please go to: Mixed Numbers and Improper Fractions.
I had found a visual on Mixed Numbers from The Mailbox Magazine:
I liked this little bit of help! Anything that I can use to help my students remember the steps makes me happy! In fact, I explained that changing a mixed number into an improper fraction was also like doing a somersault (you move your way around the fraction).
When we turned to improper fractions to mixed numbers, we did not have a fun little helper. This time, I explained that this set of steps is more like a backflip (you flip from the denominator up into the numerator: divide).
Once we had taken our notes, we went to the IXL website to work on solving these kinds of problems. If you would like to practice at home, there are two links:
We will continue to practice our new skills tomorrow.
HOMEWORK: FINISH Countdown 2.2 and the writing prompt on the back.
Decompose the procedure for solving this problem and simplifying your answer:
5/12 + 4/9
Friday, January 23, 2015
Adding and Subtracting Mixed Number
Today we continued working with addition and subtraction of fractions. However, today we worked with adding and subtracting fractions that were mixed numbers (a whole number with a fraction).
In the process of adding and subtracting our mixed numbers, we came across an answer that was an improper fraction. I have not taught the procedure to convert mixed to improper or improper to mixed (that is on the books for Monday), so I am accepting answers in the form of improper fractions for today, since I want to introduce and work with one concept at a time! (I will know better for next year...I should have known better this year!)
Anyway, we worked in table groups again today as we are still becoming comfortable with the process of adding and subtracting fractions. There are a lot of steps to remember!
- find the LCD of the two fractions using factor trees and venn diagrams
- convert the fractions into equivalent fractions using the LCD
- perform the operation (addition or subtraction)
- determine if the answer needs to be simplified
- use factor trees and venn diagrams to find the GCF
- simplify the fraction
To get these steps down so that we are comfortable takes practice, practice, and more practice!
I did solve a few problems with the classes to give examples of adding and subtracting mixed numbers. To view this please watch the video: Adding and Subtracting Mixed Numbers.
Thursday, January 22, 2015
Adding and Subtracting Fractions with Unlike Denominators (continued)
Today was a continuation from our learning yesterday. We practiced adding and subtracting fractions by:
- finding the LCD (least common denominator)
- creating equivalent fractions
- performing the operation (addition or subtraction)
- evaluating our answer to determine if it is in simplest form
- simplifying any fraction not in simplest form by using our GCF (greatest common factor)
To practice, we used a sheet I found in Teacher's Helper from The Mailbox. It was in the Oct/Nov 2011 magazine, The page was titled, "One Clever Cat." I have linked the video (One Clever Cat) showing the first four problems as examples.
Wednesday, January 21, 2015
Adding and Subtracting Fraction with Unlike Denominators
We worked with adding and subtracting fractions with unlike denominators. The process can be daunting. To see my classroom examples, please watch: Adding and Subtracting Fractions with Unlike Denominators.
The process itself is:
- Use the denominators of the two fractions you are working with the find the LCD using factor trees and Venn Diagrams.
- Once you know the LCD, you now have to make equivalent fractions using your new LCD and the original fractions.
- Next, you perform the given operation.
- Now you have to determine if the answer is in simplest form.
- One way to do this is to look at the numerator. If the numerator is a prime number, you need to see if the denominator is a multiple of that prime number. If not, then you are done.
- To simplify the fraction, you need to make a factor tree for the numerator and the denominator. Find any factors that the two numbers have in common and divide by that number.
This is not an easy process to remember, so we will continue working with finding LCD, making equivalent fractions, and simplifying with GCF.
Tuesday, January 20, 2015
LCM also known as LCD (Least Common Denominator)
Today we worked with finding Least Common Denominators and then creating equivalent fractions. I asked my classes to use factor trees and Venn Diagrams to help with the process. I needed to explain that LCM and LCD are synonymous (they mean the same thing) as both are used to determine the new denominator needed for our equivalent fractions.
We practiced 12 problems as table groups and will continue working with LCD and GCF tomorrow as we begin adding and subtracting fractions and then writing our answer in simplest form.
To see examples from today's activity, please watch the video: Least Common Denominator.
HOMEWORK: Countown 1.7
Monday, January 19, 2015
LCM and GCF using Venn Diagrams
Here come the fractions! In preparation for adding and subtracting fractions, I introduced the concepts of Least Common Multiple and Greatest Common Factor.
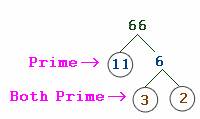
I explained that we use LCM whenever we are expected to add and subtract fractions that do not have a common denominator. However, I used two visual graphics to teach this concept instead of listing all of the factors of each of the given denomiators. We began by finding the prime factors of both of the given denominators by using a factor tree. For example:
Then we use our factor trees to place our numbers into a Venn Diagram (placing the common factors in the center). Once all of the factors from both numbers have been placed on the Venn, multiply ALL of the numbers together to find the LCM.
Once we had a common denominator, we now had to create equivalent fractions using this new denominator. Then add the fractions together to determine the answer.
Now, once we had an answer we need to simplify our fraction. To do this, we need to use the Greatest Common Factor to determine what to divide by. We began much in the same manner as LCM. We took the numerator and denominator and created factor trees. Then we placed our prime factors in a Venn Diagram. This time, however, you need only multiply the factors that are in the center section of the Venn... the ones both numbers have in common. This is the number you need to divide the numerator and denominator by to find simplest form of the fraction.
To see the notes for the lesson, follow the link:
To see additional examples, follow the link:
Thursday, January 15, 2015
Think Through Math revisit
We spent some time today revisiting Think Through Math and our goals. There were some parts of TTM that my students did not know about, so I took some time to explain them. Some of these were:
- Messages - if they have a notification of a message they need to check it. The message is usually from me.
- I explained how to look at their dashboard to understand how they are doing on TTM.
- I reminded them about our goal of Think30. Every student who passes 30 lessons by April 20 will go on a trip to visit Chuck E. Cheese and attend a movie. Also, for every 5 lessons passed, students earn a bead for their Outdoor School necklace.
Then I explained how students could use TTM to earn extra credit. The following is the email I sent home to parents explaining the extra credit as well:
Since returning from Christmas Break, there has been more math homework coming home in the form of Countdown to STAAR. This is because I am now doing either Intervention or Social Studies for 30 minutes of my class time every day. This means we lose 30 minutes of time on task.
These assignments will typically come home on Monday, Tuesday, and Thursday. They will have 6-8 questions. This means that each question is worth quite a bit. Missing one takes you to a "B". However, this is a necessary evil. The Countdown to STAAR is written specifically to address the rigor students will see the day of the STAAR (April 20). This also means that grades are lower.
I placed math grades into the grade portal today. If you have not set up viewing your student's grade portal, just contact the elementary office. They will give you the information you need to login to this valuable resource. For those of you who have been accessing the grade portal, you can see the scores your child is making on our assignments. Many times parents will ask me for extra credit assignments. One way to earn extra credit is to correct the problems that were missed for a grade of 70%. However, I have decided on a second way to allow students to earn extra credit...
To earn extra credit, your child need only work onthinkthroughmath.com at home on evenings and weekends. Now, I do not want your child to sit in front of a computer all evening. Kids need to play! However, I am able to see how much time was spent on evenings (5:00 pm - 7:00 am) and weekends and for every 45 minutes spent on the program, your child will have earned $20 PRIDE Bucks to spend in our PRIDE Store on Fridays AND a "100" in the gradebook.
Wednesday, January 14, 2015
Tuesday, January 13, 2015
Factors and Multiples
Today was a day to apply our knew knowledge and practice using our divisibility rules. I gave the students an assignment to complete working with factors and multiples called "Sign Here, Please." To see the instructions for this worksheet please follow the link.
HOMEWORK: complete "Sign Here, Please"
Monday, January 12, 2015
Divisibility Rules and Factors
Divisibility Rules are shortcuts to use when dividing by single digit numbers (and 10). They are very helpful in determining factors for numbers. Factors are two numbers that are multiplied together to make a product.
Typically, factors are used to answer the following types of questions:
- Is a number prime or composite?
- What are ALL the factors of a number?
- What factors do these two numbers have in common?
- What is the Greatest Common Factor of two numbers?
To help my students find the factors of a number, I asked them to use the Divisibility Rules and a t-chart. To watch the process, please watch the video: Divisibility Rules and Factors.
Today was our note taking, we will work with finding factors tomorrow.
HOMEWORK: Countdown 1.4
Thursday, January 8, 2015
Prime or Composite
The worksheet was titled "P. C.'s Ideal Job". It was from The Mailbox Magazine, Intermediate, Aug/Sept 2003.
We are releasing at 12:30, so we had short classes. I hope you enjoy your long weekend and GOOD LUCK to those of you participating in the Hamilton County Stock Show!
Wednesday, January 7, 2015
Sieve of Eratosthenes (Prime or Composite)
Today we worked with the Sieve of Eratosthenes. This procedure was a way to separate prime and composite numbers using their factors.
Using this information and a hundreds chart, we found the prime numbers between 2 and 100. In the process we found out some interesting facts:
A prime number has only two factors: 1 and itself.
A composite number has more than two factors.
- 1 is NEITHER prime nor composite as it only has 1 factor.
- 2 is the ONLY EVEN PRIME number.
To see our lesson and to see how the "sieve" works, please watch the video: Prime or Composite?
HOMEWORK: Countdown 1.3
Tuesday, January 6, 2015
Snowflake Critical Attributes
We began the lesson by brainstorming a list of critical attribute questions that we use in geometry to classify any shape. Our list included:
- Can it be classified as a polygon?
- How many sides?
- can it be classified as a quadrilateral?
- How many angles?
- right?
- acute?
- obtuse?
- How many vertices?
- What kinds of lines?
- parallel?
- intersecting?
- perpendicular?
- Is there symmetry?
- how many lines of symmetry?
Once we completed the list of critical attributes, we created snowflakes. Each student was given a template to use. I found the templates at http://www.daves-snowflakes.com/patterns.html Each template began as a hexagon, was folded on a line of symmetry to form a trapezoid, was folded to form a rhombus, and finally folded to form an equilateral triangle. Now, the students cut away the black areas. Each snowflake was attached to a sheet of black construction paper:
Finally, the students had to write critically about the snowflake. I did not want to read about "fun" or "cool" or "awesome." While I love hearing this words about my class, they are not mathematical words that describe our learning. So the writing prompt was:
Explain the geometry found in your snowflake by describing at least three geometric attributes.
Students were to use our list of critical attributes to guide their writing.
The snowflakes are displayed on lockers. Snow in Texas!
HOMEWORK: Countdown 1.2
Monday, January 5, 2015
Snowflake Geometry
Snowflakes are actually very mathematical!
Our goal today was that the students would be able to generate geometric definitions using critical attributes of a 2-dimensional figure.
We began by reading the book:
After reading the story, I showed a short video about Snowflake Bentley that showcases the photographs he began taking in the early 20th century. The images are pretty amazing!
Finally, we began to focus on the geometry of snowflakes by working with the fact that most snowflakes are hexagonal. We defined a hexagon by using its critical attributes (sides, vertices, angles, lines of symmetry, parallel, etc.), then we folded the hexagon on a line of symmetry and created a trapezoid. Next, we defined the trapezoid using its critical attributes, then folded the trapezoid to make a rhombus, and finally created an equilateral triangle, each time defining the 2-d shape using its critical attributes. I made a video of the notes that we began today entitled Snowflake Geometry.
HOMEWORK: Countdown 1.1
Subscribe to:
Posts (Atom)